Unit 9 Conic Sections Answer Key: A Comprehensive Guide to Mastery sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. Delve into the captivating world of conic sections, where curves formed by the intersection of a plane and a cone unravel their secrets.
Prepare to embark on a journey of discovery, unlocking the mysteries of circles, ellipses, parabolas, and hyperbolas.
As we delve deeper into the realm of conic sections, we will explore their defining characteristics, unravel the intricacies of their equations, and master the art of graphing these fascinating curves. Along the way, we will uncover their practical applications in diverse fields, ranging from architecture to astronomy.
With each step, our understanding of conic sections will grow, empowering us to solve complex problems and appreciate their elegance.
Unit 9 Conic Sections Overview
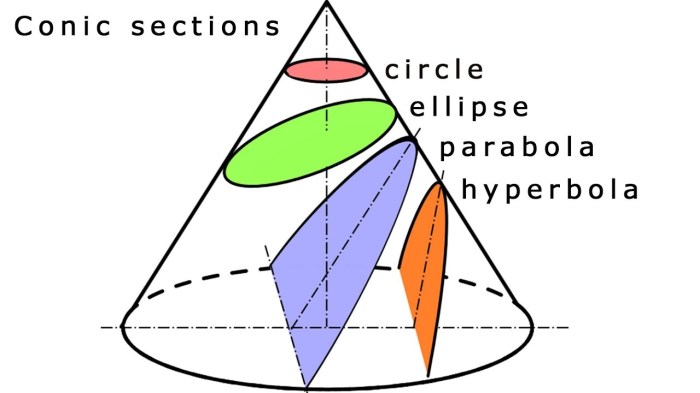
Conic sections are curves that are formed by the intersection of a plane and a cone. The different types of conic sections are circles, ellipses, parabolas, and hyperbolas. Each type of conic section has its own unique set of characteristics, such as eccentricity, foci, and asymptotes.
Key Characteristics of Conic Sections
- Eccentricity:The eccentricity of a conic section is a measure of how elongated it is. A circle has an eccentricity of 0, an ellipse has an eccentricity between 0 and 1, a parabola has an eccentricity of 1, and a hyperbola has an eccentricity greater than 1.
- Foci:The foci of a conic section are two points that are equidistant from the center of the conic section. The number of foci depends on the type of conic section: a circle has no foci, an ellipse has two foci, a parabola has one focus, and a hyperbola has two foci.
- Asymptotes:The asymptotes of a conic section are two lines that the conic section approaches but never intersects. Parabolas and hyperbolas have asymptotes, while circles and ellipses do not.
Equations of Conic Sections
The general equation for a conic section in standard form is Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0. The coefficients of the equation determine the type of conic section. For example, if A = C and B = 0, then the conic section is a circle.
If A ≠ C or B ≠ 0, then the conic section is an ellipse. If A = 0 or C = 0, then the conic section is a parabola. If A + C = 0, then the conic section is a hyperbola.
Examples of Conic Section Equations, Unit 9 conic sections answer key
- Circle:x^2 + y^2 = 9
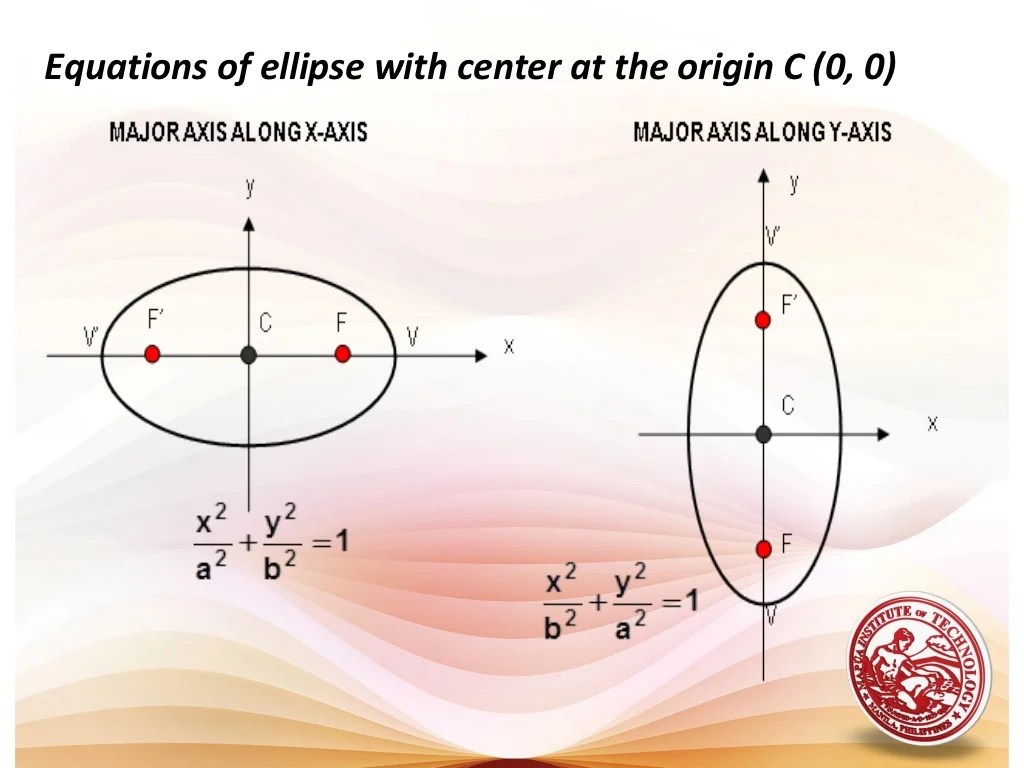
- Ellipse:4x^2 + 9y^2 = 36
- Parabola:y = x^2
- Hyperbola:4x^2 – 9y^2 = 36
Graphing Conic Sections
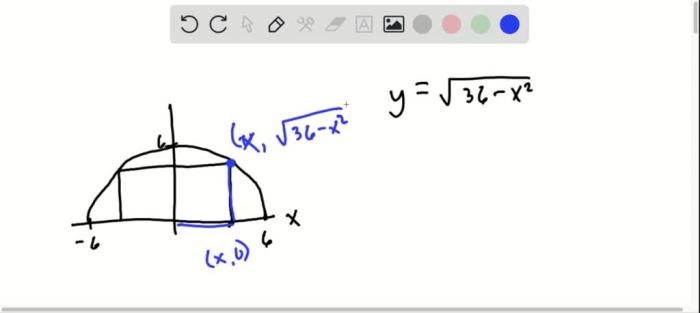
To graph a conic section, first find the center of the conic section. The center is the point (h, k) where the equation of the conic section is equal to zero. Once you have found the center, you can use the following steps to graph the conic section:
- Circles:Draw a circle with radius r = sqrt(A + C) centered at (h, k).
- Ellipses:Draw an ellipse with semi-major axis a = sqrt(A) and semi-minor axis b = sqrt(C) centered at (h, k).
- Parabolas:Draw a parabola with vertex (h, k) and axis of symmetry x = h or y = k.
- Hyperbolas:Draw a hyperbola with vertices (h ± a, k) and asymptotes y = mx ± b, where m = sqrt((A
- C) / (A + C)) and b = h
- mk.
Applications of Conic Sections
Conic sections have a wide range of applications in various fields, including:
- Architecture:Conic sections are used to design arches, domes, and other architectural structures.
- Engineering:Conic sections are used to design bridges, roads, and other engineering structures.
- Physics:Conic sections are used to describe the orbits of planets and other celestial bodies.
- Astronomy:Conic sections are used to design telescopes and other astronomical instruments.
General Inquiries: Unit 9 Conic Sections Answer Key
What is the general equation for a conic section in standard form?
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
How can I identify the type of conic section based on the coefficients of the equation?
By examining the signs and values of the coefficients, you can determine whether the conic section is a circle, ellipse, parabola, or hyperbola.
What are the key characteristics of an ellipse?
An ellipse has two foci, two vertices, and two asymptotes. Its eccentricity is between 0 and 1, and it is not a parabola or hyperbola.